.ep.gif)
Error evaluation and propagation have become a routine matter in geochronology and isotope geology, but have not attracted adequate attention in trace element determination and modelling (Dalrymple and Lanphere, 1969; Faure, 1986; Wilson, 1989). For isotope ratios, precision is generally estimated in each sample run (expressed as 2sE), but can also be determined by replicate analyses. Accuracy is also controlled by running an "accepted" standard several times during the course of a study. For trace elements, on the other hand, the precision and accuracy are generally estimated by analysing an international geochemical reference sample. The errors of trace element determination in geological samples are therefore not precisely known. However, it is not really difficult to estimate the precision of individual analysis, using error propagation theory (Bevington, 1969; Verma, 1995), as has been done for MSID (Verma, 1981; Verma and Schilling, 1982). Solid-liquid partition coefficients employed in trace element modelling are also known to vary within wide limits. The consequences of the experimental errors inherent in the determination of trace elements and partition coefficients have not been evaluated for modelling igneous processes. I present here two simple cases of partial melting and fractional crystallisation equations (Allègre and Minster, 1978).
Trace element behaviour during partial melting can be modelled from eqs. (1) and (2)..ep.gif)
As an example, for an incompatible element with a partition coefficient D0 = 0.1 (sD0 = 0.005), an original concentration in the source C0 = 1 ppm (sC0 = 0.05 ppm), one can estimate from the above eqs. that the concentration of this element in the liquid will be Cl = 5.26 ± 0.30 ppm for F = 0.1 (10% melting) and 3.57 ± 0.19 ppm for F = 0.2 (20% melting).
Similarly, the error for fractional crystallisation eq. (3) can be estimated from eq. (4).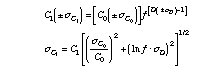
For an incompatible element during fractional crystallisation (e.g., D = 0.1, C0 = 1 ppm, sD = 0.005,sC0 = 0.05 ppm), its concentration in the residual liquid will be
Cl = 1.11 ± 0.05 ppm for f = 0.9 (i.e., after 10% crystallisation), and 1.25 ± 0.05 ppm for f = 0.8 (after 20% crystallisation).
I will show the implications of these equations in several diagrams and extend these considerations to other cases describing trace element behaviour during igneous processes.
Allègre, C.J. & Minster, J.F., Earth Planet. Sci. Lett. 38, 1-25 (1978).
Bevington, P.R., Data Reduction and Error Analysis for the Physical Sciences (McGraw, New York, 1969).
Dalrymple, G.B. & Lanphere, M.A., Potassium-Argon Dating (Freeman, San Francisco, 1969).
Faure, G., Principles of Isotope Geology (Wiley, New York, 1986).
Verma, S.P., Geostand. Newslett. 5, 129-131 (1981).
Verma, S.P., Actas Inageq 1, 215-220 (1995).
Verma, S.P. & Schilling, J.-G., J. Geophys. Res. 87, 10838-10856 (1982).
Wilson, M., Igneous Petrogenesis. A Global Tectonic Approach (Harper Collins, London, 1989).