.tiff222.gif)
Compositions of coexisting minerals from mantle xenoliths using ICP-MS allow the determination the mineral/melt partition coefficients (Kd) for Grn, Opx and Phl. The composition of coexisting liquids was calculated with the Kd's Cpx/melt (Hart and Dunn, 1993). All xenoliths are of magmatic origin but the last minerals seem to have crystallized from more evolved melt fractions. This is visible in variable inclinations of the slopes of REE patterns and their inflections found for phlogopites and some clinopyroxenes. In thuch procedure analytical error for the experimental Kd's multipleis on the error of mineral analyses which is very low (1-5% for REE).Hence the resulting Kd's should not differ much from the experimental data.
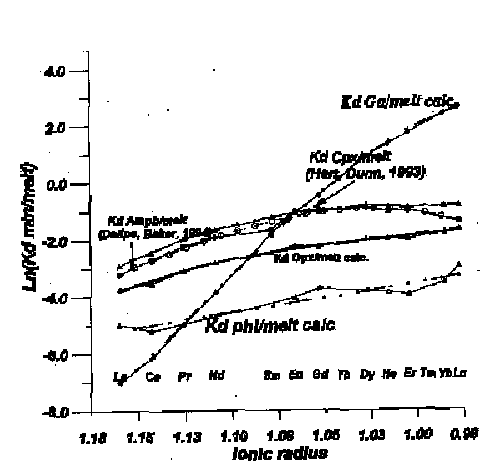
The average data for Grn Kd's, and for Phl and OPx from the most equilibrated associations are presented in Table.1. They are close to known Kd's for garnets, phlogopites and orthopyroxenes. Advantage of this procedure is in the possibility to calculate Kd's for a broader range of elements. Obtained and calculated coefficients were plotted on standard REE and spider diagrams in the order of incompatibility without any normalization. At the REE pattern they show very smooth lines similar in shape to the normalized patterns of concentration. On the spider diagram several correlating peaks for Pb, Sr positive for phlogopite and negative for garnet are visible. Garnets have also negative Th and phlogopites have positive Ba anomalies. They vary in absolute values and may be of different nature determined by influence of CO2, variations of pressure and so on as well as disequilibrium with clinopyroxenes. But the main reason is that they fill other sites in the mineral structures. Some of them agree with available experimental data for example Ba for Phl, (Foley, 1994), Sr for garnets (Sweeney et al., 1995) etc. On the diagram Ionic radius--Ln(Kd) REE partition coefficients were plotted together with those experimentally determined for Cpx/L (Hart and Dunn, 1993) and Amph/L (Dallpe and Baker, 1994). The dependence of Ln(Kd min/melt) upon the ionic radii (Fig. 1) for all minerals can be well approximated by a third-order polynomial of the general type: Ln(Kd)=a(ir-b)3+c. The last coefficient is very close to 0; b is ranging from 0.96 to 1.18 and refers to the ionic radius which corresponds to the inflection (in Ln(Kd) line). Coefficient a determines the inclination of the slope of the REE pattern. It is higher for minerals with dense structures such as Grt and lower for Amph, Phl. The above equation describe REE distribution in the minerals. Thus Kd mineral/melt can be determined by the relation of the ionic volume of an element and the volume of the structural position which the element enters.
Dallpe, C. & Baker, D.R., Mineralogical Magazine 58A, 207-209 (1994).
Foley, S.F., Jenner, G.A., Jackson, S.F. & Freyer, B.J., Mineralogical Magazine 58A, 280-281 (1994).
Hart, S.R. & Dunn, T., Contrib. Mineral. Petrol. 113, 1-8 (1993).
Sweeney, R.J., Prozesky, V. & Przybylowich, W., Geochim. Cosmochim. Acta in press (1995)..tiff222.gif)

Fig. 1: Dependence of Ln (Kd min/melt) from ionic radius.